Probability Statistics Formula Sheet: Your Ultimate Guide

Introduction

Probability and statistics are like the dynamic duo of the math world. They dance together to help us make sense of uncertainty. Whether it’s a scientist trying to predict weather patterns, a business analyst forecasting sales, or a social scientist studying trends in human behavior, these concepts play a vital role.

So, what’s the deal with probability? It’s all about measuring the likelihood of events happening. Think of it as the math behind your gut feelings. Now, statistics? It’s the art of making sense of data. It helps us summarize information, draw conclusions, and even make predictions. Together, they form the backbone of data-driven decision-making in countless fields.

Now, how do we make this complex world of numbers a bit easier to digest? Enter the probability statistics formula sheet! This handy tool serves as a quick reference guide, allowing you to grasp and apply these concepts with ease. Whether you’re prepping for an exam, working on a project, or just curious about the numbers behind daily life, a formula sheet simplifies the process.

If you’re looking for a comprehensive resource to help you navigate the world of statistics, check out Probability and Statistics For Dummies. It’s packed with insights and is perfect for anyone looking to get a grip on the fundamentals!

The purpose of this article is to provide you with a comprehensive probability statistics formula sheet. We won’t just throw formulas at you; we’ll explain what they mean and provide examples. By the end, you’ll have a solid grasp of the essential formulas and their applications. So, let’s get cracking and make probability and statistics your new best friends!

Understanding Probability and Statistics

What is Probability?

Probability is the measure of how likely an event is to occur. It’s expressed as a number between 0 and 1. A probability of 0 means the event will not happen, while a probability of 1 means it will definitely happen. Imagine you’re flipping a coin. There are two possible outcomes: heads or tails. The probability of getting heads is 0.5, and so is the probability of tails.

Key terms in probability include events, sample space, and outcomes. The sample space is the set of all possible outcomes. For our coin toss, the sample space is {heads, tails}. An event is any specific outcome or a group of outcomes. For example, getting heads is one event, while getting either heads or tails is another.

The significance of probability stretches across various real-world scenarios. From predicting weather conditions to assessing risks in finance, understanding probability helps us make informed decisions. Business owners use it to forecast sales, while doctors rely on it to determine treatment effectiveness. It’s a powerful tool that turns uncertainty into a calculable metric.

For those eager to dive deeper into probability, consider picking up Probability: For the Enthusiastic Beginner. This book makes the complex concepts of probability more accessible and fun!

What is Statistics?

Statistics is the science of collecting, analyzing, and interpreting data. It helps us organize raw data into a meaningful form. Statistics can be broadly divided into two categories: descriptive and inferential statistics.

Descriptive statistics summarize data. They provide simple summaries and visualizations, like mean, median, and mode. For example, if you have test scores for a class, descriptive statistics can tell you the average score or the most common score. For more insights on descriptive statistics, check out this comprehensive guide.

Descriptive statistics are essential for summarizing and visualizing data effectively. Learn more about their applications in manufacturing.

Inferential statistics, on the other hand, allow us to make predictions or inferences about a larger population based on a sample. It involves hypothesis testing and estimation. For instance, if you want to know the average height of all high school students in a city, you might measure just a few hundred students. Inferential statistics help you make educated guesses about the entire population based on that sample.

Statistics plays a crucial role in data analysis and decision-making. Businesses analyze customer data to improve sales strategies, while researchers use statistics to validate their findings. In a world overflowing with data, mastering statistics is essential for making sense of it all.

If you’re interested in a more structured approach to learning statistics, check out Essentials of Statistics. This book covers all the foundational concepts you need to know!

Descriptive Statistics

Key Concepts in Descriptive Statistics

Descriptive statistics are the unsung heroes of data analysis. They provide a way to summarize and understand the key features of a dataset without diving into complex calculations. Two main categories reign supreme: measures of central tendency and measures of variability.

Measures of Central Tendency give us a snapshot of where the center of our data lies. The mean, median, and mode are the three musketeers here.

– The mean is simply the average value. You calculate it by adding all numbers together and dividing by the total count.

– The median is the middle value when the data is sorted. If you have an odd number of values, it’s the center one; if even, it’s the average of the two center values. For a detailed exploration of median statistics, refer to this resource.

The median is a vital measure of central tendency that provides insight into data distribution. Discover more about median salary insights in Poland.

– The mode is the value that appears most frequently. A dataset may have one mode, more than one mode, or none at all. For additional information on mode and its applications, check out this comprehensive guide.

Understanding the mode helps in identifying trends in data. Read more about statsmodels and residuals.

Measures of Variability tell us how spread out the data is. They include the range, variance, and standard deviation.

– The range is the difference between the highest and lowest values in the dataset. For insights on crime statistics related to range, visit this overview of Orange County crime statistics.

The range provides a quick assessment of data spread. Explore the crime statistics in Orange County for more context.

– Variance measures how much the values deviate from the mean. A high variance indicates that data points are widely spread out.

– The standard deviation is the square root of the variance. It provides a more intuitive measure of variability, as it’s in the same units as the original data.

Common Formulas

Mean, Median, Mode

– Mean:
Mean = \(\frac{\sum_{i=1}^{n} x_i}{n}\)
Example: For the dataset [2, 3, 5, 7], the mean is (2+3+5+7)/4 = 4.25.

– Median:
– If n is odd:
Median = x_{\left(\frac{n+1}{2}\right)}
– If n is even:
Median = \(\frac{x_{\left(\frac{n}{2}\right)} + x_{\left(\frac{n}{2}+1\right)}}{2}\)
Example: For [2, 3, 5, 7, 9], the median is 5. For [2, 3, 5, 7], the median is (3+5)/2 = 4.

– Mode:
– Simply the value that appears most often.
Example: In [2, 2, 3, 5], the mode is 2.

Variance and Standard Deviation

– Variance:
Variance = \(\frac{\sum_{i=1}^{n} (x_i – \text{Mean})^2}{n}\)
Importance: Variance helps in understanding the data’s spread. A low variance indicates that the data points tend to be close to the mean.

– Standard Deviation:
Standard Deviation = \(\sqrt{\text{Variance}}\)
Importance: Standard deviation is vital for grasping how data varies from the mean. It’s especially useful in fields like finance, where understanding risk is key.

Visualization Techniques

Visual representations can be game-changing when it comes to understanding descriptive statistics. Histograms and box plots are two popular methods.

– A histogram displays the distribution of data points across different intervals, effectively showing frequency. It’s like a bar chart, but the bars touch, illustrating data continuity.

– A box plot provides a summary of the dataset’s distribution. It shows the median, quartiles, and potential outliers, offering a quick visual insight into data spread.

These visuals enhance our understanding of descriptive statistics by providing clarity and context. They help us see the story behind the numbers, making the data not just numbers, but an engaging narrative.

Speaking of visuals, if you need a tool to create your own statistical graphics, you might want to consider using a Histogram Chart Maker. It can help bring your data to life!

Probability Distributions

Probability distributions are essential tools in statistics. They describe how probabilities are assigned to different outcomes of a random variable. Understanding these distributions helps in making informed decisions based on data. Let’s explore the various types of probability distributions, including discrete and continuous distributions, along with their common formulas.

Types of Probability Distributions

Discrete Distributions

Discrete distributions deal with countable outcomes. Two popular examples are the binomial and Poisson distributions.

Binomial Distribution: This distribution models the number of successes in a fixed number of trials. Each trial has two possible outcomes: success or failure.

The formula for the binomial probability is:
P(X = k) = \(\binom{n}{k} p^k (1-p)^{n-k}\)
where:
– n is the number of trials.
– k is the number of successes.
– p is the probability of success on each trial.
– \(\binom{n}{k}\) is the binomial coefficient.

For example, if you flip a coin 10 times, you can calculate the probability of getting exactly 5 heads using this formula.

Poisson Distribution: This distribution is used for counting the number of events in a fixed interval of time or space. It is particularly useful when the events occur independently and with a known average rate.

The formula for the Poisson probability is:
P(X = k) = \(\frac{\lambda^k e^{-\lambda}}{k!}\)
where:
– \(\lambda\) is the average rate of occurrence.
– k is the actual number of occurrences.
– e is Euler’s number (approximately 2.71828).

An example could be counting the number of emails received in an hour when you know the average is 3 emails per hour.

Continuous Distributions

Continuous distributions deal with outcomes that can take any value within a range. The normal distribution is the most commonly encountered continuous distribution in statistics.

Normal Distribution: This distribution is characterized by its bell-shaped curve. It’s significant because many statistical methods assume normality in the data.

The normal distribution is defined by two parameters: the mean (\(\mu\)) and the standard deviation (\(\sigma\)). The formula for the probability density function (PDF) of the normal distribution is:
f(x) = \(\frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x – \mu)^2}{2\sigma^2}}\)

In this formula:
– x is the variable.
– \(\mu\) is the mean.
– \(\sigma\) is the standard deviation.

The properties of the normal distribution include:
– Symmetry about the mean.
– Approximately 68% of values lie within one standard deviation of the mean.
– About 95% fall within two standard deviations.

Understanding the normal distribution provides insight into how data behaves in real-world scenarios, such as heights or test scores.

If you want a deeper understanding of probability distributions, I highly recommend The Art of Statistics: Learning from Data. It’s an excellent resource for visual learners!

Common Probability Formulas

Probability Mass Function (PMF)

For discrete random variables, the Probability Mass Function (PMF) defines the probability of each possible value. The PMF for a discrete random variable X is given by:
P(X = x) = f(x)

The PMF is crucial for discrete distributions like the binomial and Poisson, as it allows us to compute the probability of specific outcomes.

Probability Density Function (PDF)

For continuous random variables, the Probability Density Function (PDF) describes the likelihood of the variable falling within a particular range of values, rather than taking on a specific value. The PDF is defined such that:
P(a < X < b) = \(\int_{a}^{b} f(x) \, dx\)

where f(x) is the PDF of the random variable X.

The area under the curve of the PDF over a specified interval reflects the probability of the variable falling within that interval. This concept is vital in statistics, particularly when working with normal distributions and calculating probabilities for continuous data.

With these formulas and insights into probability distributions, you can confidently tackle various statistical problems. Understanding these distributions is a stepping stone to mastering the world of probability and statistics.

Inferential Statistics

Introduction to Inferential Statistics

Inferential statistics is like a crystal ball for data enthusiasts. It allows us to make educated guesses about a larger population based on a sample. Imagine you want to know how many jellybeans are in a giant jar. Instead of counting every single jellybean, you scoop out a handful and make inferences about the whole jar. This is the essence of inferential statistics!

Hypothesis testing and estimation are the two main pillars of inferential statistics. When we hypothesize, we set up claims and test them against sample data to see if they hold true. Estimation helps us predict population parameters, like means or proportions, using sample statistics. This approach is vital in fields ranging from healthcare to marketing, where making decisions based on data is crucial.

Key Concepts

Sampling Distributions

Sampling distributions are the backbone of inferential statistics. When you take multiple samples from a population, the means of those samples form their own distribution. This is where the Central Limit Theorem (CLT) shines. The CLT states that, regardless of the population’s distribution, the means of sufficiently large samples will be normally distributed. This magical theorem allows us to make inferences about the population mean using the sample mean. For a deeper understanding of the Central Limit Theorem, refer to this article.

The Central Limit Theorem is fundamental in statistics, providing a foundation for making inferences. Learn more about its importance here.

To better grasp sampling distributions, we need formulas for the standard error and confidence intervals.

– Standard Error (SE) is calculated as:
SE = \(\frac{\sigma}{\sqrt{n}}\)
where \(\sigma\) is the population standard deviation and n is the sample size. The standard error gives us an idea of how far the sample mean is likely to be from the population mean.

– Confidence Interval (CI) provides a range of values within which we expect the true population parameter to fall. The formula for a confidence interval for the mean is:
CI = \(\bar{x} \pm z \cdot SE\)
where \(\bar{x}\) is the sample mean and z is the z-score corresponding to the desired confidence level (like 1.96 for 95% confidence). This interval helps us quantify the uncertainty around our estimates.

Hypothesis Testing

Hypothesis testing is like a trial for our assumptions. We start with two competing claims: the null hypothesis (H0) and the alternative hypothesis (H1). The null hypothesis typically states that there is no effect or difference. In contrast, the alternative hypothesis suggests that there is an effect or difference. For a comprehensive overview of hypothesis testing, refer to this cheat sheet.

Hypothesis testing is a critical aspect of inferential statistics. Discover more about the testing process and its applications.

Now, let’s look at some key formulas used in hypothesis testing.

1. T-tests are used to compare means between two groups. The formula for the t-statistic is:
t = \(\frac{\bar{x}_1 – \bar{x}_2}{SE}\)
where \(\bar{x}_1\) and \(\bar{x}_2\) are the sample means, and SE is the standard error of the difference between the means. Use a t-test when the sample sizes are small or when the population standard deviation is unknown.

2. Chi-square tests assess relationships between categorical variables. The formula is:
\(\chi^2 = \sum \frac{(O – E)^2}{E}\)
where O is the observed frequency and E is the expected frequency. This test helps determine whether observed data fits a particular distribution.

Knowing when to use these tests is crucial. Use t-tests for comparing means and chi-square tests for categorical data analysis.

Conclusion of Inferential Statistics

Inferential statistics plays a pivotal role in making predictions and decisions based on sample data. It empowers researchers and analysts to draw conclusions about a population without needing to survey everyone. By employing sampling distributions, hypothesis testing, and estimation techniques, we can navigate uncertainty with confidence.

In today’s data-driven world, mastering inferential statistics is essential. It enables informed decision-making, enhances research findings, and contributes to advancements in various fields. So the next time you encounter a sample, remember: you have the power to infer, estimate, and make a difference!

Comprehensive Probability Statistics Formula Sheet

A well-organized probability statistics formula sheet is a lifesaver for students and professionals alike. This handy reference will categorize essential formulas into three main sections: descriptive statistics, probability distributions, and inferential statistics. Each category contains key formulas and brief explanations to help you quickly find what you need.

Descriptive Statistics

Formula	Description
Mean (\( \bar{x} \))	The average of a dataset. Calculated as \( \bar{x} = \frac{\sum x_i}{n} \)
Median	Middle value of a sorted dataset. If n is odd, Median = x_{\left(\frac{n+1}{2}\right)}; if even, Median = \frac{x_{\left(\frac{n}{2}\right)} + x_{\left(\frac{n}{2}+1\right)}}{2}
Mode	The value that appears most frequently in the dataset.
Variance (\( \sigma^2 \))	Measures dispersion: \( \sigma^2 = \frac{\sum (x_i – \bar{x})^2}{n} \)
Standard Deviation (\( \sigma \))	Square root of variance: \( \sigma = \sqrt{\sigma^2} \)
Range	Difference between highest and lowest values: Range = x_{\text{max}} – x_{\text{min}}

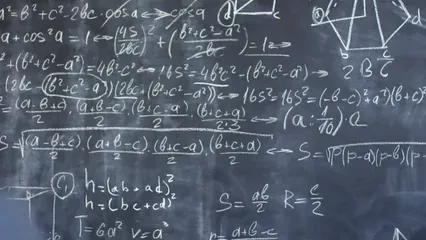
Probability Distributions

Formula	Description
Probability Mass Function (PMF)	For discrete variables: P(X = x) = f(x)
Binomial Distribution	P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} for n trials.
Poisson Distribution	P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!} for k occurrences.
Probability Density Function (PDF)	For continuous variables: P(a < X < b) = \int_{a}^{b} f(x) \, dx
Normal Distribution	f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x – \mu)^2}{2\sigma^2}}

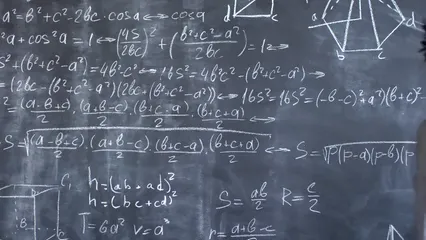
Inferential Statistics

Formula	Description
Standard Error (SE)	SE = \frac{\sigma}{\sqrt{n}}
Confidence Interval (CI)	CI = \bar{x} \pm z \cdot SE
T-test	t = \frac{\bar{x}_1 – \bar{x}_2}{SE} for comparing two means.
Chi-square Test	\chi^2 = \sum \frac{(O – E)^2}{E} for categorical data analysis.

This formula sheet is your go-to resource for essential statistics concepts. Use it wisely, and you’ll navigate the world of probability and statistics with ease!

Conclusion

Mastering probability and statistics is like learning to ride a bike. At first, it seems daunting, but once you get the hang of it, it becomes second nature. Understanding these concepts is crucial for students and professionals across various fields. Whether you’re crunching numbers in business, conducting research in social sciences, or even analyzing sports data, a solid grasp of these statistical tools will serve you well.

The formula sheet provided here is more than just a collection of equations. It’s a valuable resource that can help you make sense of data, draw conclusions, and ultimately inform your decisions. Keep it handy for quick reference while studying or working on projects.

Don’t forget to practice! The best way to internalize these formulas is by applying them to real-world data. Start with simple datasets, and as you grow more confident, tackle more complex analyses. You’ll not only improve your statistical skills but also enhance your ability to interpret and communicate data effectively. So grab that formula sheet and get to work—your future self will thank you!

FAQs

Please let us know what you think about our content by leaving a comment down below!

Thank you for reading till here 🙂

All images from Pexels